Is the Ultimate Dice Roller _Mathematically_ Fair?
Hey everyone,
The other day, @ecoinstant posed an excellent question about the Ultimate Dice Roller: we know it's provably fair, but is it mathematically fair? In other words, over a large number of rolls, does it produce a statistically even distribution?
I thought that was a great question to dig into. To test it, I added some scripts to the project's GitHub repository to simulate rolling 3d6 thousands of time. A 3d6 roll is common for generating character stats in old-school D&D, and it should produce a nice bell curve distribution of results from 3 to 18.
Test 1: 100 Rolls, As Fast as Possible
First, I had the script roll 100 times as quickly as possible. Because the rolls happen so fast, they all use the same seed data from the same Hive block. The result was, as expected, not very random at all.
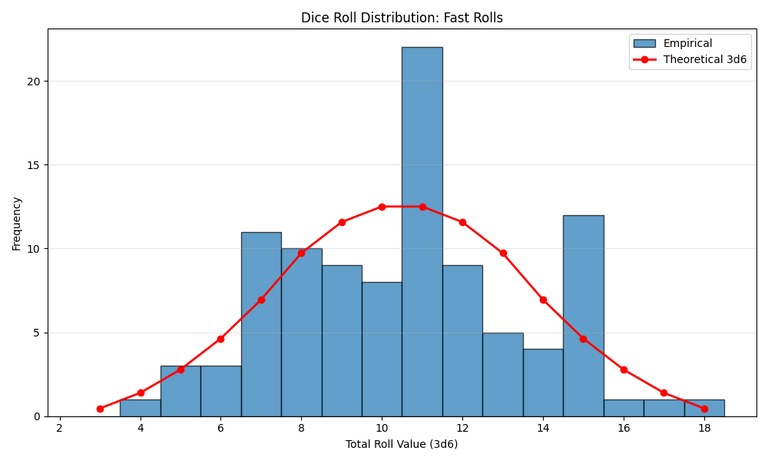
Test 2: 100 Rolls, With a Delay
Next, I had the script wait a few seconds between each of the 100 rolls. This pause allows the blockchain to produce new blocks, ensuring that each roll gets a new, unique seed (server seed, client seed, and nonce). The result was a much better, more varied distribution.
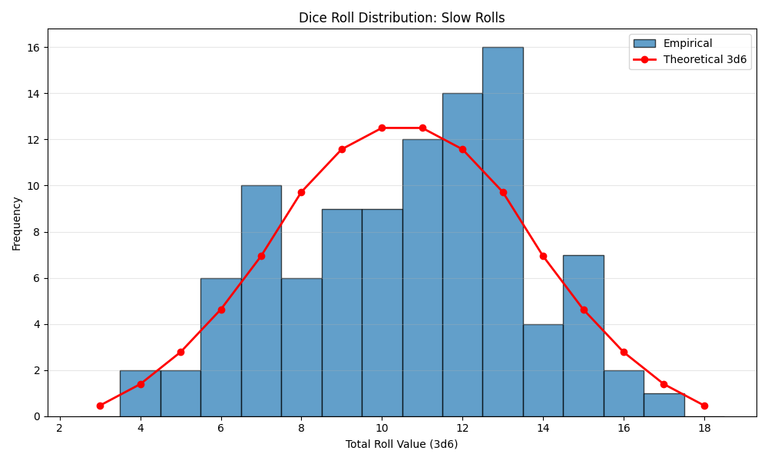
Test 3: 5,000 Rolls
Finally, for the ultimate test, I had the script roll the dice 5,000 times. I did this as fast as possible because waiting a few seconds for each roll would have taken over four hours (5,000 rolls x 3 seconds/roll ≈ 4.16 hours). The script rapidly requested rolls, and the server's "salting" mechanism ensured each roll was still unique even if the block data was the same.
The final chart speaks for itself.
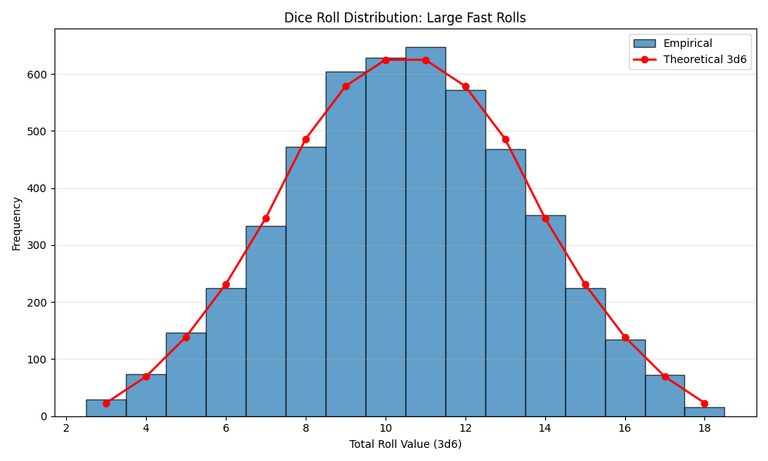
With a large enough sample size, the dice roller produces a beautiful, statistically fair bell curve, right on the money. So, the answer is yes, the Ultimate Dice Roller is not only provably fair but mathematically fair as well.
If this kind of statistical analysis interests you, feel free to take a look at the scripts directory in the GitHub repo to see how the tests were run and the plots were generated.
As always,
Michael Garcia a.k.a. TheCrazyGM

I love this - a Hive utility that can cross over into the real world.
I'll get a friend to try it, he's notorious for having cursed dice 😆
Normal distribution is a measurement of randomness only on a large scale, and is not relevant to individual players. It does not help if 5000 numbers are randomly distributed, if, for example, you get the same combination 5 runs in a row. I'd recommend that you look at the entropy.
How do I measure entropy?
https://nvlpubs.nist.gov/nistpubs/Legacy/SP/nistspecialpublication800-22r1a.pdf
$PIZZA slices delivered:
@ecoinstant(1/20) tipped @thecrazygm
Come get MOONed!
This is interesting. And it definitely shows that our salting method is mathematically fair. Somehow, I still think we need to let it roll dice for a week and track, what if the blockchain itself is biased somehow?
!PAKX
!PIMP
!PIZZA
View or trade
PAKXtokens.Use !PAKX command if you hold enough balance to call for a @pakx vote on worthy posts! More details available on PAKX Blog.
I'll write up a cron job to run every minute or so, and just let it build the db so we can see what happens after some time goes by.
That's a fascinating test and analysis, my friend. So if it only evens out smoothly with a high number of rolls, how does that affect small numbers of rolls in row, say 10, 25, or 50? 😁 🙏 💚 ✨ 🤙
Well, even if they happen rapidly and use the same server seed, client seed, and nonce, there is a salt that is added to ensure randomness. So,they should be just fine, it's that you don't always get a proper curve on low numbers, outliers are more likely, e.g. you can flip a coin twice and get heads both times, and if that's the length of your sample, it looks skewed, you only see it when you do it a lot.
Ah, yes, I see. Thank you for the explanation, my friend, I appreciate it. 😁 🙏 💚 ✨ 🤙