Técnicas de derivación/Derivada de un producto de funciones//Derivative techniques/Derivative of a product of functions
En este post queremos deducir la técnica para derivar el producto de dos de funciones reales de variable real, g y h.
In this post we want to derive the technique to derive the product of two real functions of real variable, g and h.
Esto es:
Dadas las funciones diferenciables g y h, con dominio en
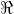.gif) (conjunto de los números reales), se quiere determinar y aplicar en ejemplos la Técnicas para derivar la función f definida por f(x)=g(x).h(x)
(conjunto de los números reales), se quiere determinar y aplicar en ejemplos la Técnicas para derivar la función f definida por f(x)=g(x).h(x)
That is:
Given differentiable functions g and h, with domain in.
(set of real numbers), we want to determine and apply in examples the Techniques for deriving the function f defined by f(x)=g(x).h(x)
Comencemos // Let's start
Usemos la definición de derivada para deducir la técnica, esto es:// Let us use the definition of derivative to derive the technique, that is:
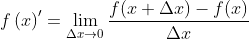.gif)
Donde f(x)=g(x).h(x), por lo que nuestra expresión anterior, queda así:// Where f(x)=g(x).h(x), so our previous expression, remains as follows:
.gif)
Apliquemos la definición de producto de funciones en la expresión anterior:// Let us apply the definition of product of functions in the previous expression:
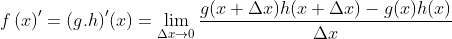.gif)
Restemos y sumemos al numerador, la expresión g(x+Δx).h(x)// Let us subtract and add to the numerator, the expression g(x+Δx).h(x)
.gif)
Factorizando, este límite queda así:// Factoring, this limit looks like this:
.gif)
Aplicando suma de límites, nos queda así://Applying sum of limits, we are left with the following:
.gif)
Por ser g es diferenciable en x entonces g es continua en x, de donde:// Since g is differentiable in x then g is continuous in x, hence:
.gif)
De esta forma://In this way:
.gif)
Y así, la fórmula deseada es la siguiente:// And so, the desired formula is as follows:
.gif)
Vamos ahora un ejemplo de aplicación:// Let's go now to an application example:
Consideremos las funciones siguientes://Consider the following functions:
.gif)
Solución://Solution:
Derivemos las funciones h y g así:// Let us derive the functions h and g as follows:
.gif)
Luego apliquemos la fórmula obtenida para la derivada de un producto://Then let's apply the formula obtained for the derivative of a product:
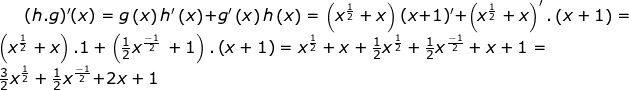.gif)
♥♣♥♥♣♥♥♣♥♥♣♥♥♣♥
Créditos
Usamos el Editor de Ecuaciones LaTeX para editar las ecuaciones.
El contenido es totalmente original.
Credits
We use the LaTeX Equation Editor to edit the equations.
The content is completely original.
♥♣♥♥♣♥♥♣♥♥♣♥♥♣♥
Posted with STEMGeeks

Su post ha sido valorado por @ramonycajal
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.