Ungleichung mit zwei Beträgen lösen

Kommt in einer Ungleichung mehr als ein Betrag vor, so ist eine Verkettung von Fallunterscheidungen notwendig.
Dieses Beispiel ist etwas komplizierter, sodass ich eine Übersicht erstellt habe, um die Fallunterscheidungen besser zu veranschaulichen. Auch für die Vereinigung der Lösungsmenge kann eine Tabelle helfen.

Zuerst kümmern wir uns um den ersten Betrag |x+1|. Dafür gibt es zwei Fallunterscheidungen. Einmal x>=-1 (Fall 1) und x<-1 (Fall 2).
Im ersten Fall dürfen wir die Betragszeichen weglassen und die Gleichung vereinfachen. Nun kümmern wir uns um die "inneren" Fälle. Also, x>=3 (Fall 1A) und x<3 (Fall 1B).
Für die beiden inneren Fälle wird die Lösung bestimmt. Da es sich auch noch um eine Ungleichung handelt muss die maximale Bedingung erfüllt werden.

Als Beispiel: In Fall 1A lautet die Lösung x>=2/3. Nun muss diese Lösung mit den Bedingungen für Fall 1A und Fall 1 übereinstimmen. Man sucht nach der Schnittmenge aus x>=2/3 (Lösung Fall 1A), x>=3 (Bedinung Fall 1A) und x>=-1 (Bedingung Fall 1) und erhält das Intervall [3;unendlich) als Lösung für Fall 1A.
Dasselbe macht man für den Fall 1B, Fall 2A und Fall 2B.
Zum Schluss wird noch die Vereinigung aller Intervalle gebildet, um die endgültige Lösung zu erhalten.

Die Betragsungleichung

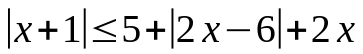
Fallunterscheidungen

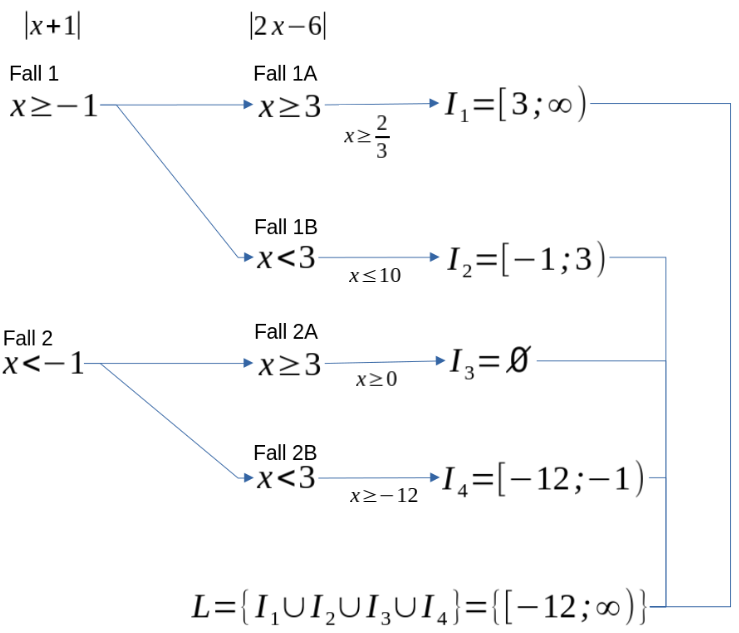
Mein Lösungsvorschlag

These photos were taken with my smartphone