Linearkombination (Vektorraum)

Nachdem wir uns die Definition und ein Beispiel eines Vektorraumes angesehen haben, soll es heute um die Linearkombination gehen.
Um eine Linearkombination aus den Vektoren aus einem Vektorraum V bilden zu können, benötigen wir noch n Elemente aus einem Körper K. Oftmals handelt es sich dabei um reelle Zahlen.
Diese Vektoren werden mit den Elementen aus dem Körper multipliziert und diese Summe ergibt wiederum einen neuen Vektor.

Sehen wir uns mal die Definition und ein Beispiel dazu an. Als Beispiel dienen Vektoren mit jeweils 4 Elementen.
Diese vier Vektoren werden mit einem Skalar multipliziert und die Summe aus diesen vier Vektoren ergibt dann einen neuen Vektor, in diesem Fall den Vektor L.
Natürlich ist dieses Beispiel nur eine Möglichkeit. Sicherlich wird es noch andere Skalare geben, mit denen sich der Vektor L darstellen lässt.

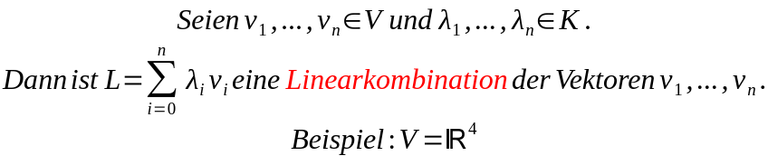
These photos were taken with my smartphone