Limes, Grenzwertrechnung

Der Limes ist der Wert dem sich eine Funktion oder eine Folge an einer bestimmten Stelle annähert, aber nicht erreicht. Man nennt es auch den Grenzwert einer Folge oder einer Funktion.

Unter dem Limes steht die Variable und daneben mit einem Pfeil der Wert wo das Verhalten der Funktion untersucht werden soll.
Das erste Beispiel ist eine Polynomfunktion 3. Grades. Bei Polynomfunktionen untersucht man die größte vorkommende Potenz. Nun schaut man was passiert, wenn x ein immer größeren Wert annimmt. Der Wert geht zunächst gegen plus unendlich. Das negative Vorzeichen sorgt aber dafür, dass der Wert gegen minus unendlich läuft. Somit ist der Grenzwert minus unendlich.

Beispiel 2 ist eine gebrochen rationale Funktion. In diesem Beispiel klammern wir die größte Potenz aus. Das sorgt dafür dass die ausgeklammerte Variable teilweise im Nenner steht, denn negative Potenzen kann man als Bruch schreiben.
Wenn eine Variable im Nenner steht und im Zähler nur eine Konstante, so ist der Grenzwert für x gegen unendlich 0. Nun fassen wir den Rest zusammen und kommen auf ein schönes Ergebnis von 1/3 hoch 20 was der Grenzwert ist.

Bei dem dritten Beispiel muss man aufpassen. Die Limes kann nicht nur gegen unendlich oder minus unendlich gehen, sondern auch gegen einen bestimmten Wert. Hier kommt noch hinzu das man sich vom positiven aus der 2 näheren soll. Wer den Funktionsgraphen zu 1/x kennt, der weiss das an der Polstelle 0 zwei verschiedene Grenzwerte sind, je nachdem ob man sich der 0 vom negativen oder vom positiven nähert. Hier ist es genauso. In diesem Fall ist der Grenzwert (plus) unendlich.

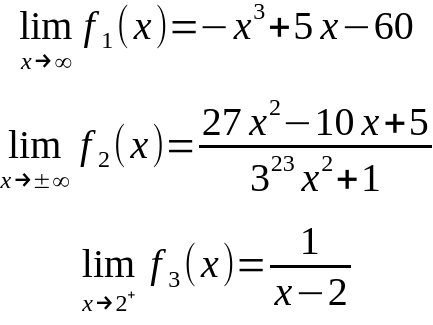
These photos were taken with my smartphone