Understanding Degeneracy in Quantum Chemistry: Exploring 1D, 2D and 3D Box Models | ChemFam #85 |
Greetings everyone! In my last blog, we have studied about zero point energy. We have checked the ZPE for all three cases, that is 1D, 2D and 3D box. After ZPE, today we shall discuss about an another very important topic called degeneracy. Degeneracy is a fundamental concept that plays a crucial role in understanding the behavior of particles confined within certain potentials.
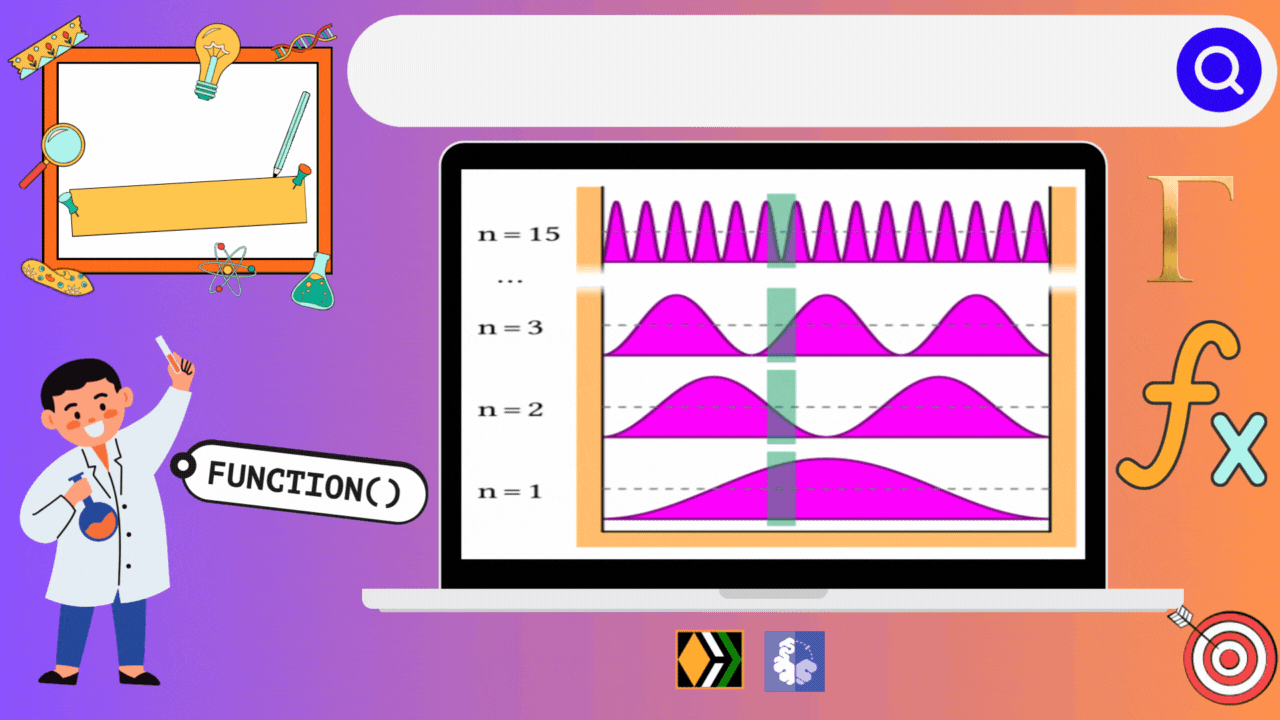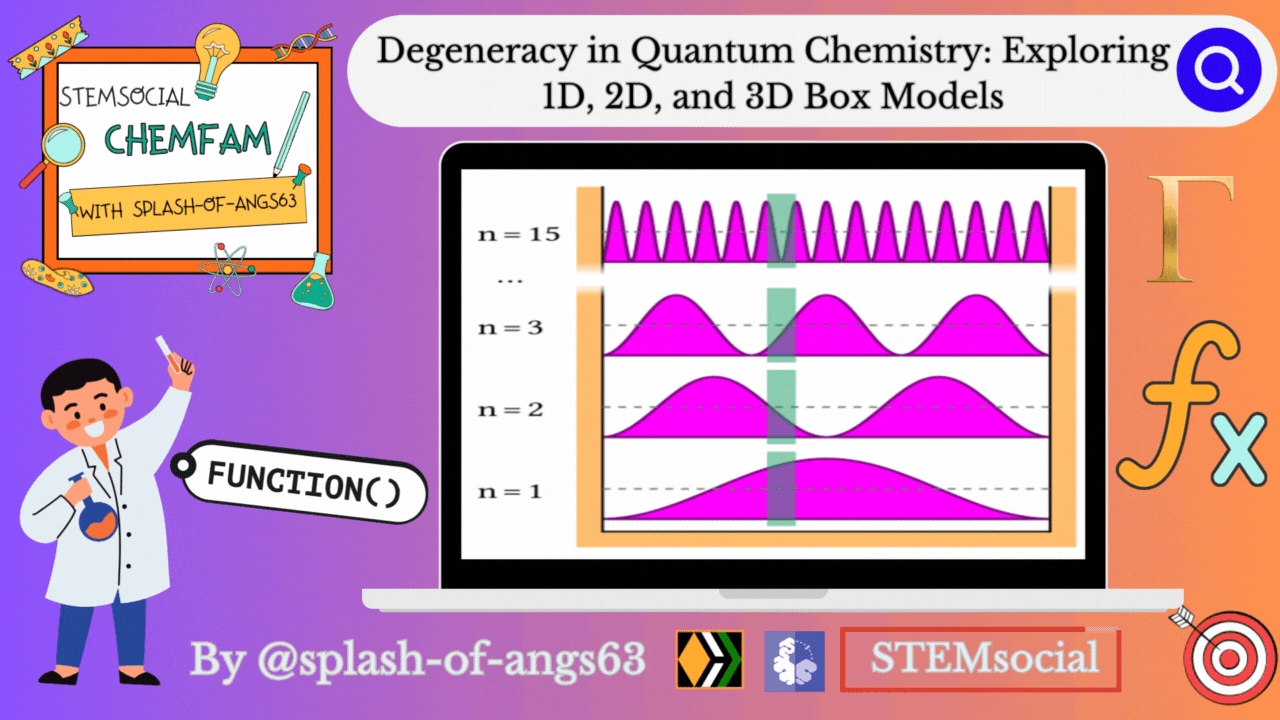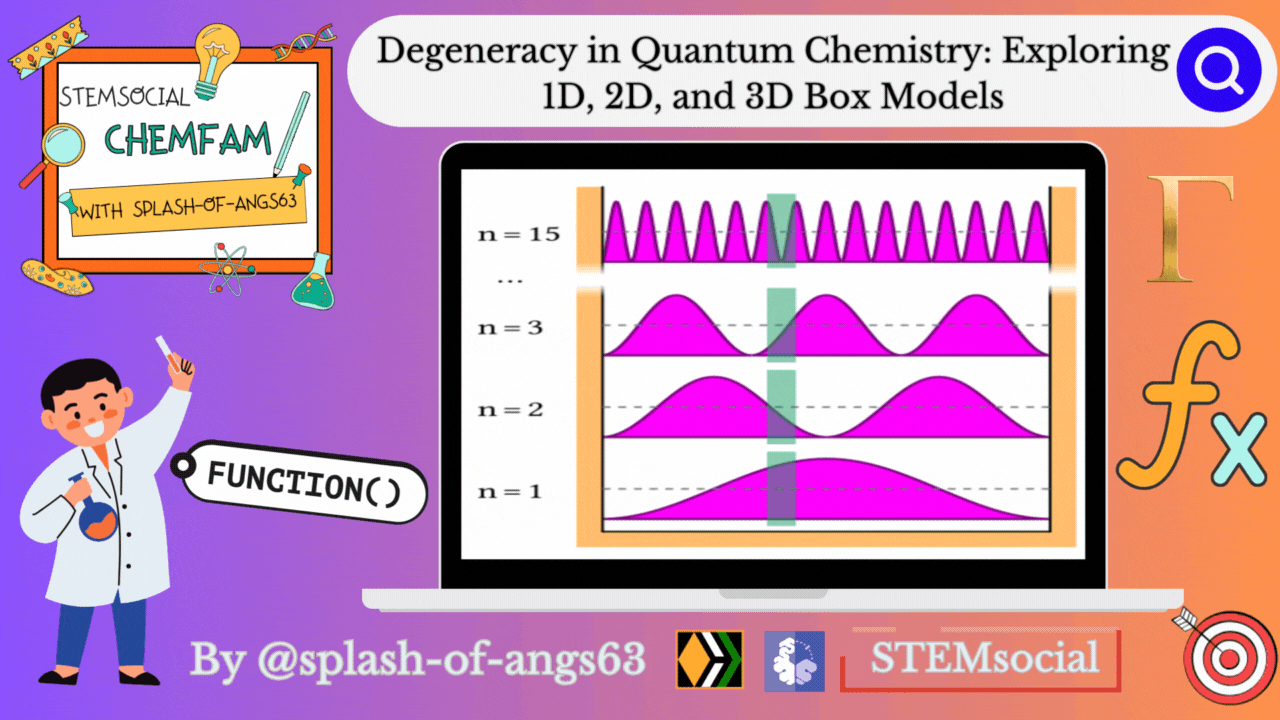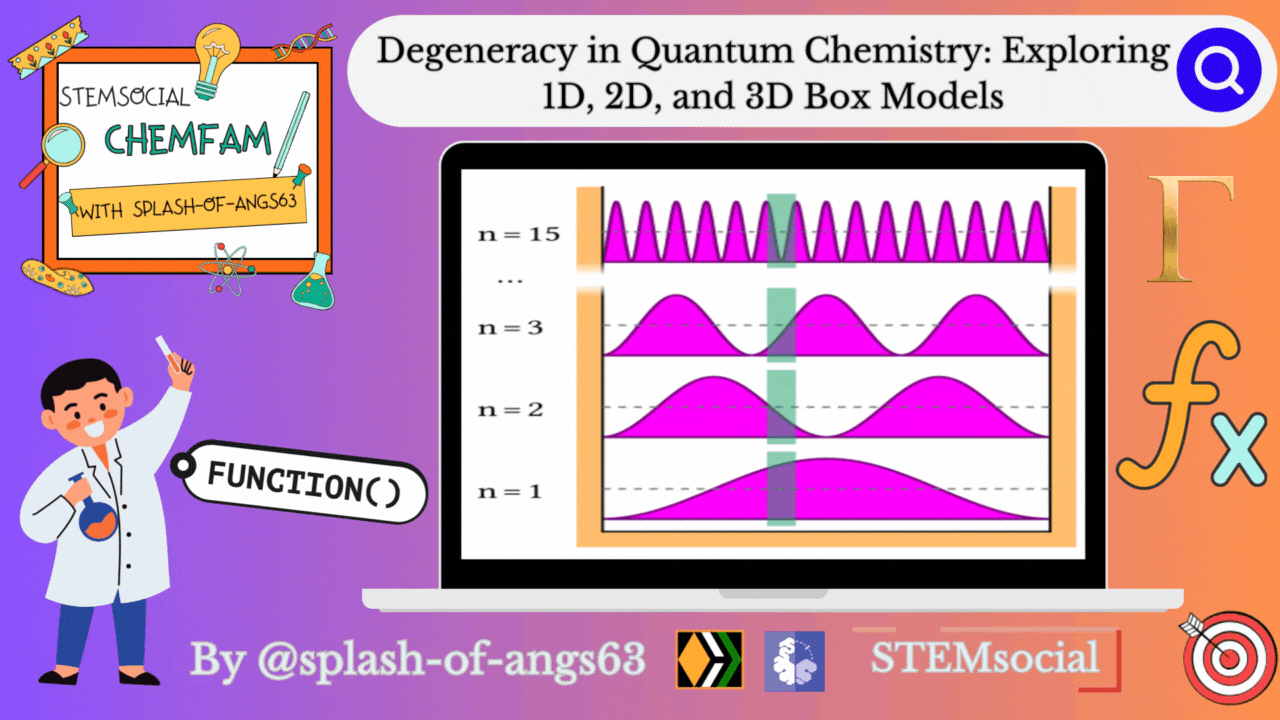
Imagine you're playing a game where you have to fit a ball inside different types of boxes. Each box has its own rules, and depending on those rules, the ball can move in different ways and have different amounts of energy. In the world of quantum mechanics, particles behave similarly when they're confined in what we call "boxes," but instead of balls, we're dealing with tiny particles like electrons.
In quantum mechanics, an energy level is degenerate if it corresponds to two or more different measured states of a quantum system. In contrast, a quantum mechanical system is said to be degenerate if two or more different states of the system give the same energy value when measured. The number of different states relative to a given energy is called the degeneracy of that energy. In classical mechanics, this can be understood as different orbits corresponding to the same energy. Degeneracy plays an important role in quantum statistical mechanics.
Degeneracy holds profound implications, influencing various phenomena in chemistry, physics, and materials science. One of the simplest yet illustrative systems to comprehend degeneracy is the particle in a box model, which can be extended to one, two, or three dimensions.
Degeneracy for particle in a 1D box
In our first case, we have a simple one-dimensional box, like a narrow tunnel where the ball can only move back and forth. Each time the ball moves, it gains a certain amount of energy, but it has to follow specific rules dictated by the tunnel's length and the ball's mass. Interestingly, in this tunnel, each energy level corresponds to a unique state of the ball. So, there's no confusion – each energy level is like a unique room where the ball can be found.

As you can see from the above data, all the energy levels are discrete and have a degeneracy of 1. That is no two energy states have the same energy value.
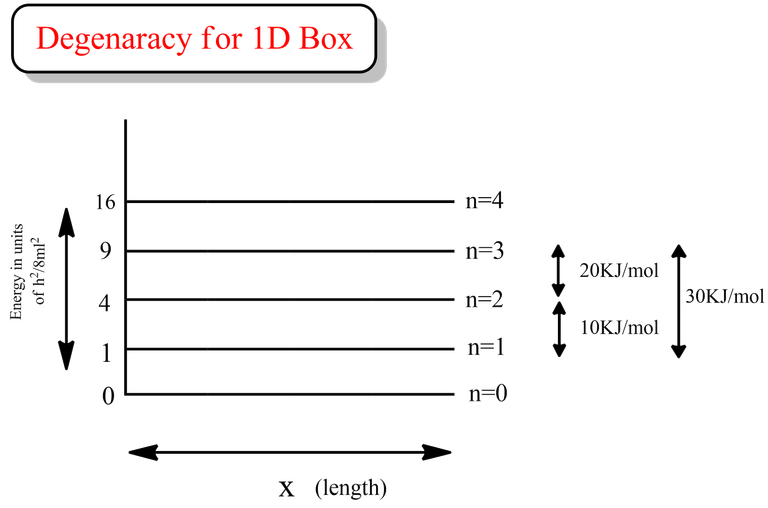
Something interesting could be seen from the diagram that I have drawn above. The energy difference (ΔE) between n=3 and n=1 is say 30 KJ/mol. So, even if we provide a cumulative energy of 27 KJ/mol from n=1 state, the particle will still be at the quantum state corresponding to n=2, as there is no separate energy levels for 27 KJ/mol. This basically relates the quantization of energy phenomenon.
Degeneracy for particle in a 2D box
Now, let's spice things up a bit with a two-dimensional box, like a flat square room. Here, the ball can move not only left and right but also up and down. With this extra freedom, things get more interesting. The energy levels now depend on how the ball moves in both directions. Sometimes, different combinations of movements give the ball the same amount of energy. It's like having different paths to reach the same floor in a building – each path may look different, but they all lead to the same place. This phenomenon is called degeneracy – where different paths (or combinations of movements in our case) lead to the same energy level.
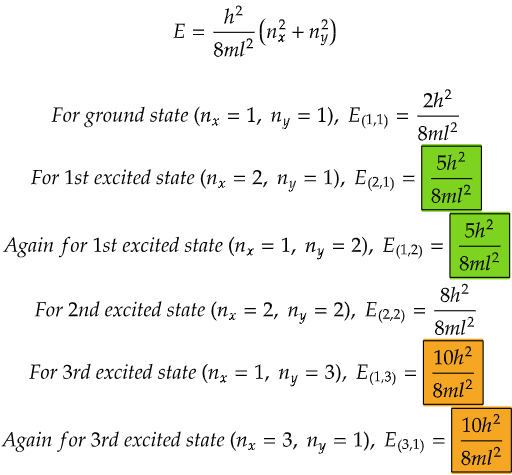
From the data above, we can see that both the energy levels in the case for first excited state (highlighted in green) and both the energy levels for 3rd excited state (highlighted in orange) are same respectively.
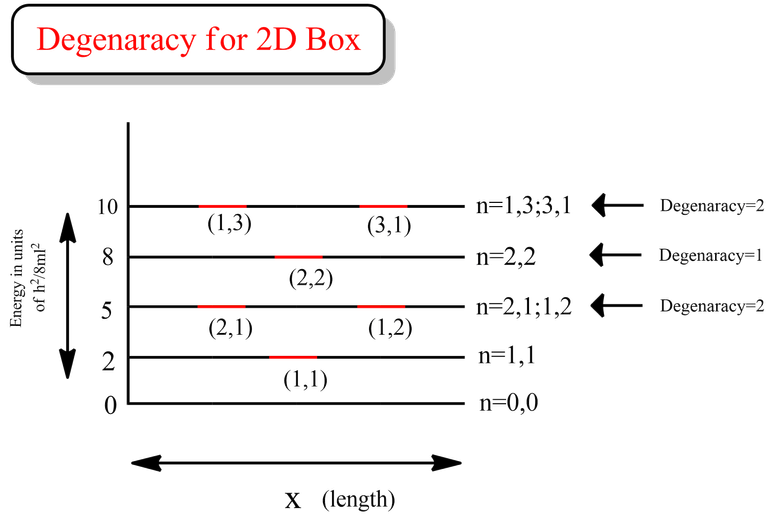
That clearly indicates that the degeneracy for 1st and 3rd excited state is 2 for the case of particle in a 2D box.
Degeneracy for particle in a 3D box
Lastly, let's imagine a three-dimensional box, like a big cube with plenty of room for the ball to roam freely in all directions. Now, the ball can move not just left, right, up, and down, but also forward and backward. With all this freedom, the number of possible energy levels increases even more, and so does the chance of degeneracy. Different combinations of movements in three dimensions can lead to the same amount of energy, creating a variety of paths for the ball to follow.
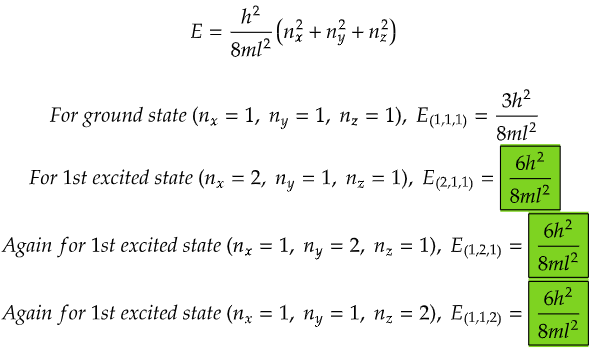
From the data above, we can see that all the energy levels in the case for first excited state (highlighted in green) are same. Similarly if we calculate, we will get the same degenerate energy levels for 2nd and 3rd excited states.
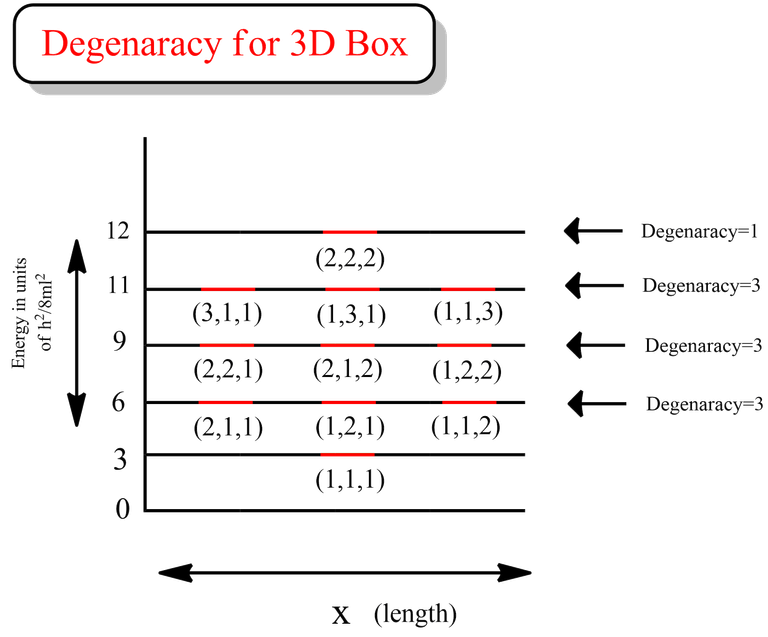
That clearly indicates that the degeneracy for 1st, 2nd and 3rd excited state is 3 for the case of particle in a 3D box.
Tips and Tricks
From the discussions above and what we have seen, we can make few points to help us to find the number of degeneracy.
- If nx=ny=nz, then degeneracy=1
- If nx=ny≠nz, then degeneracy=3
- If nx≠ny≠nz, then degeneracy=6
What we learnt?
We learnt what degeneracy means and saw that there exists degenerate or same energy levels for different arrangements.
Understanding degeneracy isn't just about playing games with balls and boxes; it has real-world implications, especially in chemistry and physics. Knowing how particles behave when confined in different spaces helps us understand the behavior of atoms, molecules, and materials. It's like solving a puzzle – knowing which energy levels are degenerate allows scientists to predict how particles will interact, how substances will behave under different conditions, and even how light and energy are absorbed and emitted.
We summarized the learning through few tips and tricks at the end
Software used:
The mathematical equations are prepared using mathcha.io editor and diagrams are drawn using ChemDraw software.

If you like my work and would like to support me, you can do so by joining my fanbase by clicking this link
Introduction to Zero Point Energy and its Cases in Particle in a Box | ChemFam #84 |
Quantum Confinement : Particle in a 2D box and 3D box | ChemFam #83 |
Molecular Chirality: A Mirror Image Perspective | ChemFam #82|
Exploring Time-Independent Schrödinger's Wave Equation and Particle in a 1D Box | ChemFam #80 |
The Role of Gamma Function in Quantum Mechanics | ChemFam #79 |
Postulates of Quantum Mechanics and Normalization of Wavefunction |ChemFam #78|
Understanding Commutator Relations and Exploring Eigenfunctions in Quantum Mechanics |ChemFam #77|
How to find Expression of an Operator and Commutation Relations |ChemFam #76|
Basics to Quantum Chemistry: Operators, Functions and Properties of Operators |ChemFam #75|
A Comprehensive Study of Euler's Reciprocal Rule in Thermodynamics |ChemFam #73|
A Deep Dive into Nutrition Essentials: Your Path to a Healthier, Happier You |ChemFam #72|
Decoding Liver Function Tests through Chemistry |ChemFam #71|
Understanding the Dynamic Roles of Metalloenzymes and Metal-Activated Enzymes |ChemFam #70|
Cracking the Thermal Code: Differential Thermal Analysis in Modern Research |ChemFam #69|
Applications and Importance of IR Spectroscopy: Shedding Light on Molecular Structures |ChemFam #68|
PS The thumbnail image is being created by me using canva.com
Games I play on Hive
| Games I play on Hive | Game description |
|---|---|
| Terracore | Terracore is an Idle mining game based on Hive blockchain |
| Rise of the Pixels | ROTP is a Web3 browser game about game development on Hive |



It’s fascinating to see degeneracy explained with such clarity, especially using the particle-in-a-box analogy. Your post reminds me of how detailed models and simulations help solidify these concepts in STEM education. For example, exploring related topics like energy quantization and movement constraints, as seen here: https://edubirdie.com/docs/virtual-high-school/stem-chemistry/46846-sled-wars-gizmo-answer-key, can make abstract quantum ideas more relatable. Integrating these tools in teaching can bridge the gap between theoretical knowledge and practical application, inspiring students to dive deeper into complex subjects like quantum mechanics. Keep up the excellent work in breaking down these intricate topics for broader understanding.
Your comment is upvoted by @topcomment
More info - Support @topcomment - Discord
Damn, bro. What a nerd! hehe
P.S Now imagine a 4 Dimensional box and calculate its degeneracy (whatever that is...lol)
Haha bro!
That could be done too! (never seen anyone doing that, haha); but since energy is additive in nature we can just add the 4th dimension's quantum state(say, 'a') and it should go like, E=h2/8ml2(nx2+ny2+nz2+na2) 😉
I repeat, WHAT A NERD!!!
View more
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
Thanks for including @stemsocial as a beneficiary, which gives you stronger support.
!hiqvote
@splash-of-angs63, the HiQ Smart Bot has recognized your request (1/3) and will start the voting trail.
In addition, @splash-of-angs63 gets !PIZZA from @hiq.redaktion.
For further questions, check out https://hiq-hive.com or join our Discord. And don't forget to vote HiQs fucking Witness! 😻